Stable power processes are never guaranteed. An assortment of unstable behaviors wrecks power apparatus, including mechanical vibration, malfunctioning control apparatus, unstable fluid flow, unstable boiling of liquids, or combinations thereof.
"INHERENTLY SAFE" REACTORS AREN'T SAFEThe experts tell us that they will build "safe" reactors, using inherent reactor characteristics to limit any unwanted rise in reactor power. A rise in power increases the temperature of reactor parts, causing them to swell, or bend, or otherwise distort. A necessary condition for stable reactor power stable is that the reactor distortion accompanying a temperature rise decrease the reactivity, thus slowing any further rise in power. For instance, the reactor distortion caused by a temperature rise could allow more neutrons to be wasted by leakage, thus decreasing the reactivity. Overly simple equations for reactor power dynamics indicate that this idea should work, and sometimes it does.
The supposition that satisfying the above condition guarantees power stability is based on a false assumption that the reactor distortion occurs simultaneously with the temperature rise which caused it. The distortion lags behind the temperature change by a time determined by the mechanical dynamics of the reactor system. Therefore the change in reactivity also lags behind the temperature change, raising the possibility of unstable power oscillations. This conclusion is supported by actual experience with seriously unstable reactors such as the inoperable Ft. St. Vrain power reactor discussed later.
It is shown in the last section of this pamphlet that stability against power oscillations depends on having sufficient mechanical friction in the distorting reactor parts. Guaranteeing this requirement may be outside the power of a designer.
EVIDENCE OF REACTOR INSTABILITYMy interest in the subject of reactor instability was aroused by two sets of experiments.
I heard of the first set of experiments, called "teasing the dragon," from a physicist who had worked on the atomic bomb project. In a low-level simulation of a bomb test, a sudden pulse of nuclear energy was initiated, sufficient to cause parts of the test assembly to jump apart momentarily (and occasionally to destroy the experimenter, but not quite enough to destroy the apparatus and its surroundings). I wanted to understand how the dynamic mechanism which controlled the energy pulse might be related to the control of reactor power.
The second set of experiments, under the acronym, SPERT, was carried out at the National Reactor Test Station to study transients of reactor power. An assembly of thin sheets of aluminum bearing the nuclear fuel was immersed in a pool of water, the surface of the water being open to the atmosphere. Reactor power was slowly increased by gradually pulling out control rods. At a certain low power a spontaneous unstable oscillation suddenly appeared and built rapidly to violent proportions, resulting in a flash of blue light from Cerenkov radiation and the explosive expulsion of water from the reactor pool. The peak of power was greater by a factor of thousands than the level from which the oscillations had started. It was concluded that the unexpected instability was related to coolant boiling.
In the early 1960's I developed an analysis of a possible unstable mode of power oscillation which I thought could lead to reactor explosions. I developed mathematical criteria to try to predict the threshold of reactor power at which such unstable oscillations would occur. Based on my analyses, I concluded that coolant boiling in the SPERT reactor set up a dynamic configuration in which a heavy mass of water bounced at a low natural frequency on the soft spring provided by vapor bubbles. The mechanical oscillation was coupled with the nuclear power oscillation in an unstable combination. Water-moderated reactors, the type most commonly used for the generation of power, might be susceptible to catastrophic nuclear power oscillations if the pressure of the water in the reactor suddenly decreased, creating vapor bubbles in the core.
I wrote several reports predicting that various power reactors could be susceptible to power oscillations of the type observed in the SPERT experiments. One preliminary report entitled "Study of Reactor Kinetics" was published by the American Society of Mechanical Engineers as Paper Number 62-WA-218 late in 1961. I presented the report at the annual meeting of the Society in New York in November 1962. I received encouragement from engineering friends, but was unable to get any attention from the nuclear establishment. I was denied publication in the nuclear journals.
The internal study and public scrutiny of potential instabilities of reactor power was (and is) not popular with reactor proponents. Even when instabilities cause accidents, they are not acknowledged as such.
UNSTABLE REACTORSThe SPERT experiments seemed to us pertinent to our claim that mechanical effects contribute to reactor instability. Subsequent reactors have demonstrated instabilities similar to our predictions.
A non-nuclear model of a nuclear reactor, for a space propulsion project named ROVER, was composed of large graphite blocks through which a gas was circulated in a flow test. The blocks were restrained against the radial pressure of the gas by springs at their outer periphery. A motion picture taken during a flow test showed the blocks banging to pieces as the pressure of the circulating gas bounced them against the restraining springs in a self-excited oscillation, equivalent to a negative mechanical damping in the system. No nuclear catastrophe occurred only because there was no nuclear power to couple with the mechanical oscillation of the graphite blocks.
A high-temperature, gas-cooled reactor for electrical power was built for Colorado Public Service at Ft. St. Vrain. On completion it could not be brought to a useful level of operating power because persistent power oscillations worsened as power was increased. Because of the oscillation and other problems the reactor was abandoned. A successful ratepayers' suit removed the useless power plant from the rate base.
Other examples of unstable reactor behavior exist.
REACTOR KINETICSTwenty-five years after my failure to achieve publication in nuclear journals, my son, Bruce Thompson, volunteered to help me write a straight technical article about stability, based on a computer program which we had developed together. Our program solves by finite difference mathematics a non-linear, fourth-order differential equation involving nuclear, mechanical and thermal characteristics of reactors. Our paper, "A Model of Reactor Kinetics," was finally published in Nuclear Science and Engineering, the technical journal of the American Nuclear Society, in September 1988[1]. It demonstrates a mechanism for catastrophic instability.
Our paper demonstrates that mechanical friction in a reactor core structure, like the shock absorber in an automobile, is necessary to limit oscillations of reactor power. Without adequate internal friction, a nuclear power driven mechanical oscillation increases toward destruction of the reactor core. Design engineers in many fields have found to their sorrow that any given level of mechanical friction is difficult to guarantee. Some of the computer-generated examples later in this section show the changing core temperature and reactor power for a reactor without adequate friction to provide stability. A small perturbation in power causes an initially small oscillation which builds rapidly to destruction, either blowup or melt down.
In the design, construction and operation of nuclear reactors an attempt is made to maintain steady operation at any desired power level from fission of the nuclear fuels, uranium or plutonium. This attempt can fail, sometimes catastrophically. A nuclear power plant is a nuclear system and a mechanical system. It is also a heat-transfer system, tied in with controls, boilers, turbines, human operators and a multiplicity of other complicating factors. The possibilities for instability are myriad. This fiercely complicated set of systems is such as to preclude any possibility of the formation of adequate analytical equations and their solution to guarantee the stability of power. An experimental program sufficient to eliminate the possibilities of power instability in reactors would be expected to be ruinous of both the economy and the environment. Our program covers only a small part of the complicated possibilities, and demonstrates only one type of power instability.
PERTURBATIONS TO REACTOR POWERWe outline here the calculation of the power dynamics of a reactor, based on Reference 1. We present some necessary conditions for power stability provided by nuclear physics, as analyzed by Weinberg and Wigner in Reference 3. Their analysis generated a second-order differential equation whose solution is always stable if the coefficients in the equation are all positive. Then we consider mechanical characteristics of reactors which render the nuclear analysis insufficient to assure stability. This results in a fourth-order differential equation whose stability requires not only that all coefficients be positive, but also that a relationship among the coefficients be satisfied (Routh's criterion). It turns out that, for power stability, motion of any reactor parts which affect reactivity must be sufficiently damped by mechanical friction in the moving parts.
Reactivity and stability are unavoidably affected by depletion of reactor fuels and the accumulation of "poisons" during operation. Other destabilizing effects not considered here, or anywhere else, are so numerous and so complicated in their interrelationships as to thwart human efforts to guarantee reactor stability.
EXAMPLESWe attempt with twelve examples to demonstrate some physical properties of reactors on which stability depends. The examples show the influence on power stability of: reactivity, delayed neutrons, coefficients of reactivity, mechanical inertia, friction, heat transfer.
- The defining parameters for these examples are:
A: Time interval B: Final time C: Frequency ratio, density coefficient D: Frequency ratio, temperature coefficient E: Mechanical damping F: Nuclear damping G: Initial reactivity H: Initial power ratio I: Mechanical effects on (off) J: Heat transfer on (off) K Coefficient of Heat Transfer These parameters are more precisely defined in Reference 1.
The values used for A through K, are shown with each of the computer-generated solutions.
Nuclear and Mechanical Characteristics
The first examples show the effects of the "in-built" nuclear characteristics, delayed neutrons and temperature coefficients of reactivity, which reactor proponents say will "guarantee" the stability of their new generation of "safe" reactors. The later examples show some of the destabilizing mechanical effects which may defeat both the proponents of reactors and the rest of us.
NUCLEAR PHYSICSReactivity
Reactivity is the name of the quantity which determines the rate of change of reactor power. For reactor power to be steady the reactivity must be zero. Maintaining zero reactivity requires moving "control rods" to maintain a balance among the rates of leakage and absorption of neutrons in nuclear fuel and in other reactor materials. Because the absorption and leakage of neutrons have been extensively studied, these balancing dependencies are relatively well understood.Positive reactivity causes power to rise exponentially at a rate proportional to the reactivity. Negative reactivity causes power to decrease. To change power in a planned manner, reactivity is adjusted by moving the control rods, either manually or by means of automatic controls. Partially removing a control rod is expected to increase the reactivity, causing the power to rise to a new level. Inserting a properly designed control rod farther into the reactor should, but doesn't always, lower the power level.

Example 1
Example 1 shows the effect of a relatively large initial reactivity, ignoring several important limiting effects, leading to a rapid rise to a "blowup." The unacceptable behavior which would result from a continuation of this exponential response is modified in real reactors by two important effects.
Delayed Neutrons
The first nuclear effect is that of "delayed neutrons." Of all neutrons formed in fission a small fraction (.007) are delayed by significant time periods after absorption of the fission neutrons. The delayed neutrons, not being available immediately to support a transient rise in power, act as a damping factor on transients, providing the strong beneficial effect of limiting sudden changes in power.Examples 2, 3, and 4 show the classical "damping effect" of delayed neutrons on the rise of power, ignoring the temperature coefficient of reactivity and mechanical effects. Example 3 shows the reaction to "prompt critical" reactivity, in which by definition the initial reactivity is numerically equal to the fraction of delayed neutrons (G=F=15). The initial rate of power rise continues indefinitely on a straight line. In Example 2 the addition of reactivity greater than prompt critical (G/F = 15/14) causes an exponential rise of power faster than in Example 3. Example 4 shows a "sub-critical" reaction, in which a value of reactivity less than the fraction of delayed neutrons (G/F = 15/16) leads to the leveling-off of power at a new value, P/P0=F/(G-F) = 16.

Example 2

Example 3

Example 4
Temperature Coefficient of Reactivity
The rise in temperature which accompanies a rapid rise in power generally changes the reactivity. The "temperature coefficient of reactivity" measures the effect of changing temperature on reactivity. Because power stability requires a rise in temperature to decrease the reactivity, a "negative temperature coefficient" is necessary for stability. Examples 5, 6, and 9 show the effects on power stability of including delayed neutron damping and temperature coefficients of reactivity, but neglecting all other effects.

Example 5
Example 5 shows the destabilizing effect on reactor power of a positive temperature coefficient (D= -2.0), leading to "blowup."

Example 6
Example 6 shows an oscillation of power at nuclear frequency, with a negative temperature coefficient (D=2.0) and with delayed neutron damping (F=0.20). Because of neutron damping the oscillations decrease in magnitude with time.
The effects of the nuclear factors, reactivity, delayed neutrons and temperature coefficients, are described by a non-linear second-order differential equation. This relatively simple equation predicts stable reactor power if the temperature coefficient of reactivity is negative. Neutron damping in reactors is generally relatively large, providing a strong tendency toward stability for a simple nuclear system. The real situation is more complicated, and more difficult than can be described in terms only of nuclear factors.
MECHANICAL CHARACTERISTICSMechanical Inertia and Mechanical Friction
Changes in reactor temperature also affect the density. A decrease in the density of reactor parts tends to increase the leakage of neutrons which in turn decreases the reactivity. This adds the complications of mechanical dynamics to the analysis of reactor stability. Fast density changes in a reactor structure may cause it to vibrate, and reactor power may oscillate as a result. Accounting for this effect requires adding to the temperature coefficient described above a "density coefficient of reactivity." The density coefficient couples mechanical and nuclear power oscillations. As previously mentioned, inclusion of mechanical effects requires solution of a fourth order differential equation of reactor kinetics, as opposed to the second order nuclear equation. Prediction of power stability becomes more precarious.Examples 7 through 9 and A through C demonstrate the added mechanical effects on the nuclear requirements for power stability. Any amount of mechanical friction is sufficient to damp oscillations of simple mechanical systems. But for stability with the combined mechanical and nuclear systems there is an additional requirement. Reference 1 shows that the nuclear frequency ratio, C, must be less than the product of mechanical damping, E and neutron damping, F, or in equation form, C<E*F.

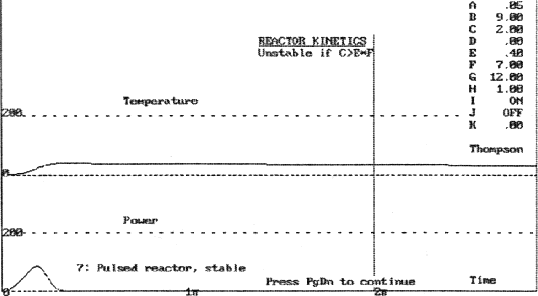
Example 7
Example 7 models a stable pulsed reactor, like those used in nuclear engineering departments at universities, and in some bomb tests. When the control rod is suddenly withdrawn, the large reactivity (G=12), above the prompt critical set by delayed neutrons (F=7), causes the temperature to overshoot the equilibrium value (G/C=6), and the power suddenly rises. Because the product of the mechanical friction (E=.4) and delayed neutron damping (F=7) is greater than the frequency ratio (C=2) as required by the stability criterion, E*F>C, the configuration is stable. After its initial burst power finally levels off near its steady state value, P/P0=1.
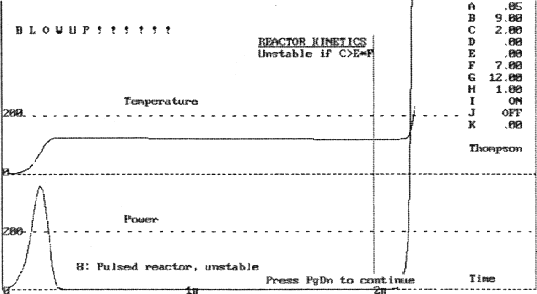
Example 8
Example 8 shows the destabilizing effect of insufficient mechanical friction on the pulsed reactor of Example 7. Because mechanical friction is zero (E=0), the value of C exceeds that allowed by the stability criterion, (C>E*F). In contrast to the leveling off shown in Example 7, bursts of energy of increasing magnitude occur at intervals of approximately 2p , in other words at the mechanical natural frequency of whatever moving reactor part is responsible for the positive density coefficient. In the intervals between peaks, energy generation becomes very small, a period in which one might mistakenly and disastrously assume that the reactor had shut down. In this example a "blowup" occurs just past the end of the first mechanical cycle.
In Examples 6 and 9 through C the scale has been expanded by a large factor to accommodate smaller transients appropriate to the operation of power reactors.
Example 9
In Example 9, with mechanical effects included, two frequencies occur simultaneously, one mechanical and the other nuclear. The nuclear frequency is twice the mechanical (D=2). Both are damped by the nuclear damping (F=.10) and mechanical damping (E=.10).

Example A
The transient in Example A shows the destabilizing effect of a positive density coefficient (C=20), with neutron damping (F=5) and a small initial reactivity (G=.05), but with inadequate mechanical damping (E=.05). This, as expected from stability analysis (C>E*F), causes power bursts at approximately mechanical frequency of ever increasing magnitude.
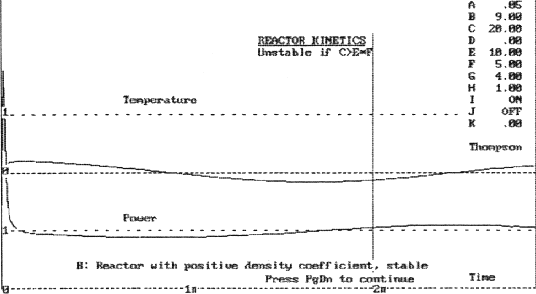
Example B
In Example B addition of sufficient mechanical damping (E=10) returns the system to stability (C<E*F), despite the larger initial reactivity (G=4).
Heat Transfer Delays the Temperature Response
When power generation in a reactor changes rapidly with time, temperature waves are propagated from fuel elements into the surroundings. Because of the time required for thermal energy to travel through materials, the temperature change at any point is delayed and reduced in magnitude depending on its distance from the surface of a fuel element and the rapidity of the power change. If the reactivity coefficients depend on the temperature and density of material at a distance from the fuel elements their effect on stability is delayed and reduced in magnitude.

Example C
Example C shows the effect of the time delay (K=1) caused by heat transfer in the heating of material distant from the fuel elements. The density coefficient of reactivity is large (C=20). The mechanical and nuclear damping are less than required for stability. Oscillations of power and temperature occur and increase in magnitude. The period of oscillation is increased by about one half by the heat transfer delay.The removal of power from a reactor requires the transfer of thermal energy through reactor materials.
CONCLUSIONSWe have discussed here some effects on stability of mechanical dynamics and heat transfer, in addition to nuclear effects. We believe that this study of REACTOR KINETICS may have pertinence to understanding, among other events, the SPERT and ROVER experiments, the oscillating power in the Ft. St. Vrain reactor, and some aspects of the accidents to SL-1 and Chernobyl.
Within the complicated systems of a nuclear power plant a multiplicity of instabilities other than those we have treated is probable. We believe a complete analysis of stability applicable to a nuclear power plant would require the inclusion of other effects too numerous and complicated for ordinary humans to handle with certainty.
Is our analysis pertinent?
So long as reactors are built, we believe the effects on stability of mechanical friction, inertia, and heat transfer outlined here should be taken into account in their design. But, because of the complication of nuclear reactors, they can never be guaranteed free from accidents. Accidents are "normal" but reactor accidents are intolerable. Because of the everlasting radioactive products it manufactures, even the "successful" reactor is intolerable.
If at the A:> prompt on my computer I type DEL *.* and press RETURN, there appears on the screen the question, Are you sure (Y/N). Because * is a wild-card, I am warned that all the information on the disk is at risk. We believe mechanical friction is a wild-card of nuclear reactors whose efficacy cannot be guaranteed by reactor designers.
We cannot afford one hundred years of automobile type make-and-break experimental development of nuclear reactors.
References:"A Model of Reactor Kinetics," by A. Stanley Thompson and Bruce R. Thompson, Nuclear Science and Engineering, September 1988. Thermal Power from Nuclear Reactors, by A. Stanley Thompson and Oliver E. Rodgers, John Wiley & Sons, Inc., New York, 1956. The Physical Theory of Neutron Chain Reactors, by Weinberg and Wigner, The University of Chicago Press, 1958, pp 603-609.
Note:
The "Reactor Kinetics" program for solving power stability problems is available for IBM clone computers, on either a 5.25 inch or a 3.5 inch floppy disk, from:
A. Stanley Thompson
1910 Monroe Street
Eugene, OR 97405
<stanleyt@efn.org>